C++中排序和复杂度

发表于 2024-12-20 分类于算法阅读次数：本文字数： 4.3k 阅读时长 ≈ 4 分钟

C++ 中排序算法详解

排序算法是计算机科学中的基础内容之一，用于按特定顺序排列元素。C++ 提供了多种排序算法，常见的排序方法包括快速排序、插入排序和希尔排序。本文将详细讲解这些排序算法的概念、实现及其时间复杂度分析。

1. 快速排序 (Quick Sort)

快速排序概述

快速排序是一种分治法（Divide and Conquer）排序算法。它通过选择一个基准元素（pivot），将待排序元素分为两部分，一部分比基准小，另一部分比基准大，然后递归地对这两部分进行排序。

快速排序的步骤：

选择一个基准元素。
将数组分成两部分：一部分包含所有小于基准的元素，另一部分包含所有大于基准的元素。
对这两部分分别进行快速排序。
最终合并所有的部分，得到有序数组。

快速排序的时间复杂度：

最佳时间复杂度：O(n log n)，当每次分割都接近均匀时。
平均时间复杂度：O(n log n)，大部分情况下。
最差时间复杂度：O(n^2)，当每次选择的基准元素都是最大或最小元素时。

快速排序代码示例：

#include <iostream>
#include <vector>
using namespace std;

// 快速排序的分区函数
int partition(vector<int>& arr, int low, int high) {
    int pivot = arr[high];  // 选择最后一个元素作为基准
    int i = low - 1;  // i是小于pivot元素的区域的分隔点

    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            i++;
            swap(arr[i], arr[j]);  // 将小于pivot的元素交换到前面
        }
    }
    swap(arr[i + 1], arr[high]);  // 将pivot放到正确的位置
    return i + 1;  // 返回pivot的索引
}

// 快速排序的递归函数
void quickSort(vector<int>& arr, int low, int high) {
    if (low < high) {
        // 找到基准元素的位置
        int pi = partition(arr, low, high);
        
        // 递归排序基准左边和右边的部分
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    vector<int> arr = {10, 7, 8, 9, 1, 5};
    int n = arr.size();
    quickSort(arr, 0, n - 1);
    
    cout << "排序后的数组：";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

解释：

partition()：用于将数组划分为两部分，并返回基准元素的最终位置。
quickSort()：递归地调用partition()，并对划分后的两部分分别进行排序。
最终，数组将被排成有序序列。

2. 插入排序 (Insertion Sort)

插入排序概述

插入排序是一种简单的排序算法，它的工作原理是将每个元素插入到已经排序的部分中。适用于小规模数据的排序，时间复杂度较低。

插入排序的步骤：

从第二个元素开始，假设第一个元素已经是排好序的。
将当前元素与前面的元素进行比较，找到合适的位置插入。
每次插入一个元素，直到所有元素都排序完成。

插入排序的时间复杂度：

最佳时间复杂度：O(n)，当数组已经排好序时。
最差时间复杂度：O(n^2)，当数组完全反向时。
平均时间复杂度：O(n^2)，常见情况。

插入排序代码示例：

#include <iostream>
#include <vector>
using namespace std;

// 插入排序函数
void insertionSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = 1; i < n; i++) {
        int key = arr[i];  // 当前要插入的元素
        int j = i - 1;
        
        // 将所有比key大的元素向右移动
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        // 插入key到正确位置
        arr[j + 1] = key;
    }
}

int main() {
    vector<int> arr = {12, 11, 13, 5, 6};
    insertionSort(arr);
    
    cout << "排序后的数组：";
    for (int i = 0; i < arr.size(); i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

解释：

每次将数组中的一个元素插入到已经排序的部分。
while循环用于移动比当前元素大的元素，找到合适的位置。

3. 希尔排序 (Shell Sort)

希尔排序概述

希尔排序是一种基于插入排序的改进算法，它通过将数组分成若干子序列来减少逆序的元素，使得插入排序在后续执行时更加高效。

希尔排序的步骤：

选择一个增量（gap），将数组分成多个子序列，每个子序列使用插入排序进行排序。
减小增量，继续对较小的子序列进行排序。
直到增量为1时，对整个数组执行一次插入排序。

希尔排序的时间复杂度：

最差时间复杂度：O(n^2)，当增量序列选择不当时。
最佳时间复杂度：O(n log n)，随着增量序列的优化，能获得更好的性能。

希尔排序代码示例：

#include <iostream>
#include <vector>
using namespace std;

// 希尔排序函数
void shellSort(vector<int>& arr) {
    int n = arr.size();
    
    // 初始增量
    for (int gap = n / 2; gap > 0; gap /= 2) {
        // 使用当前gap对数组进行插入排序
        for (int i = gap; i < n; i++) {
            int key = arr[i];
            int j = i;
            
            // 按照gap间隔进行插入排序
            while (j >= gap && arr[j - gap] > key) {
                arr[j] = arr[j - gap];
                j -= gap;
            }
            arr[j] = key;
        }
    }
}

int main() {
    vector<int> arr = {5, 2, 9, 1, 5, 6};
    shellSort(arr);
    
    cout << "排序后的数组：";
    for (int i = 0; i < arr.size(); i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

解释：

gap用于控制子序列的间隔，逐步减小增量，最终为1时进行常规插入排序。
希尔排序通过逐步减少间隔来加速排序过程，避免了大量的逆序元素。

时间复杂度概念与分析

时间复杂度 (Time Complexity)

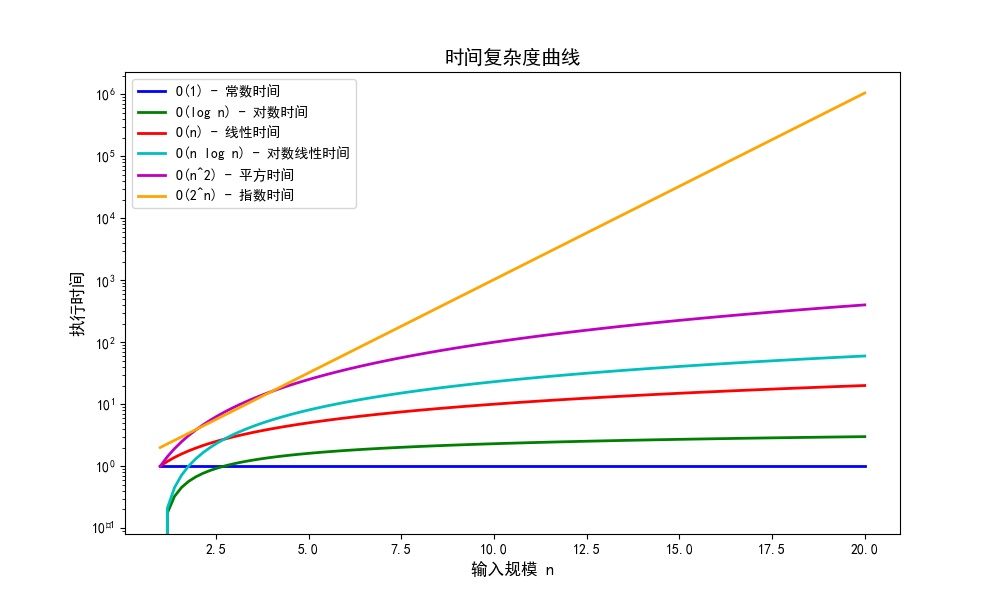
时间复杂度用于描述算法执行所需时间随输入规模（n）变化的关系。常见的时间复杂度包括：

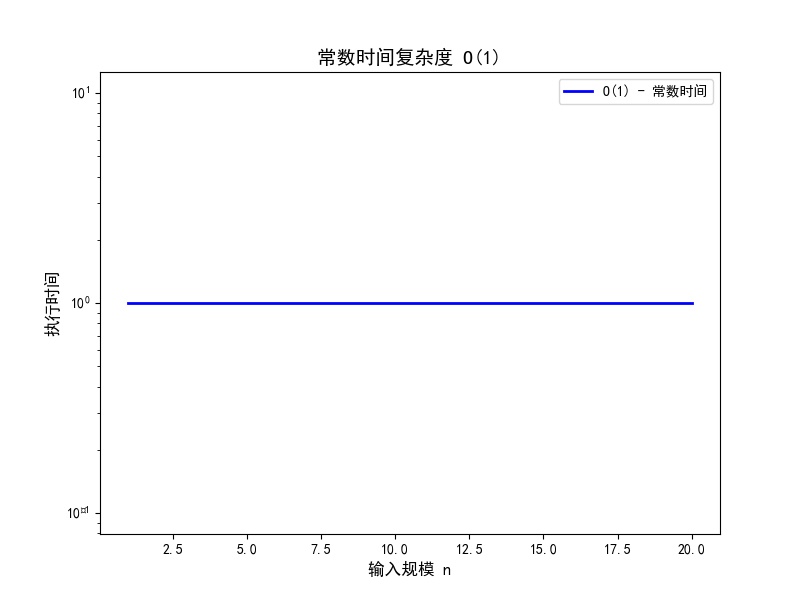
**O(1)**：常数时间，无论输入规模如何，执行时间都相同。
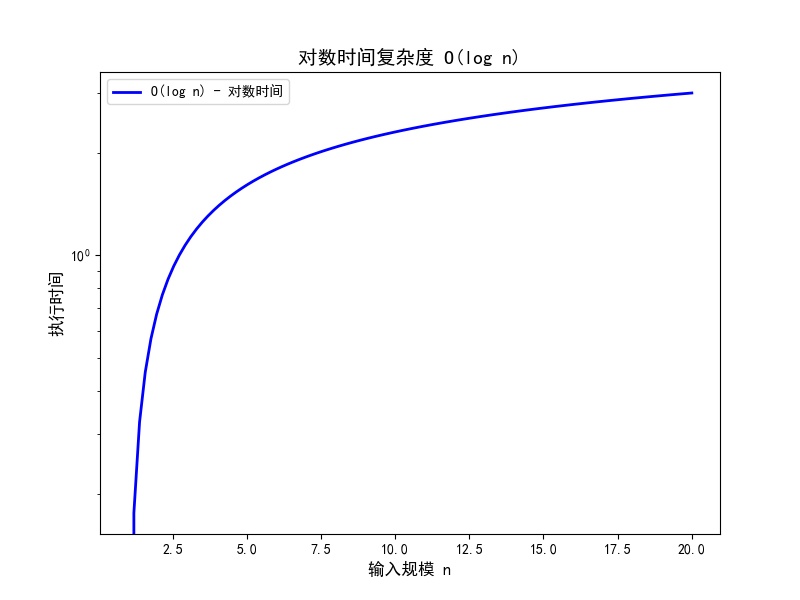
**O(log n)**：对数时间，增长较慢，常见于二分查找等算法。
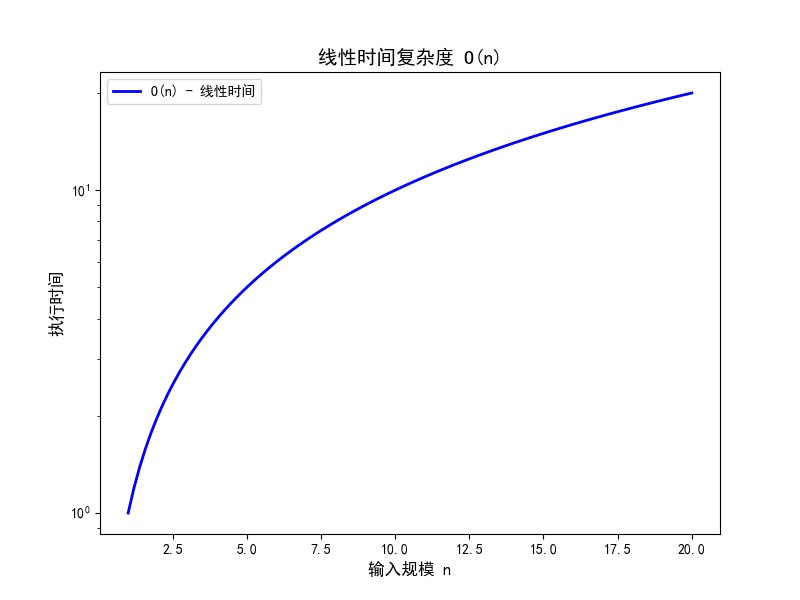
**O(n)**：线性时间，执行时间与输入规模成正比。
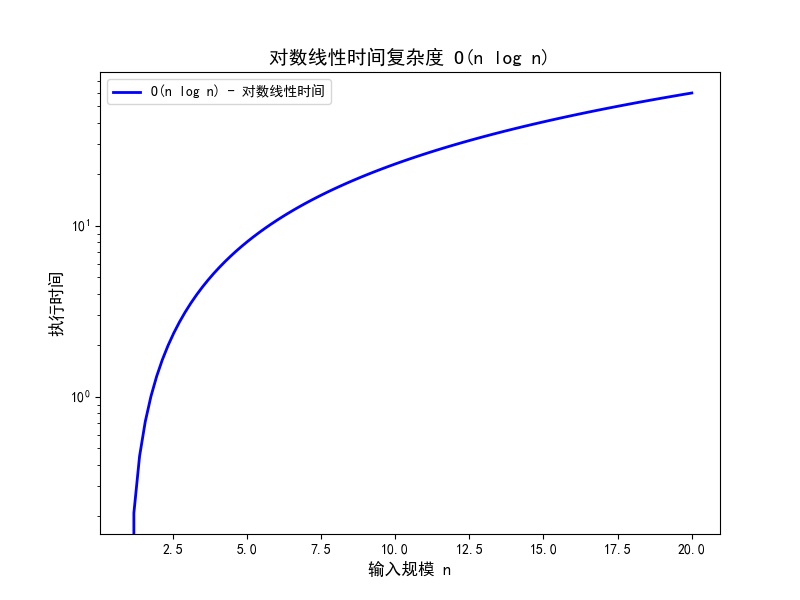
**O(n log n)**：对数线性时间，常见于高效排序算法，如快速排序、归并排序等。
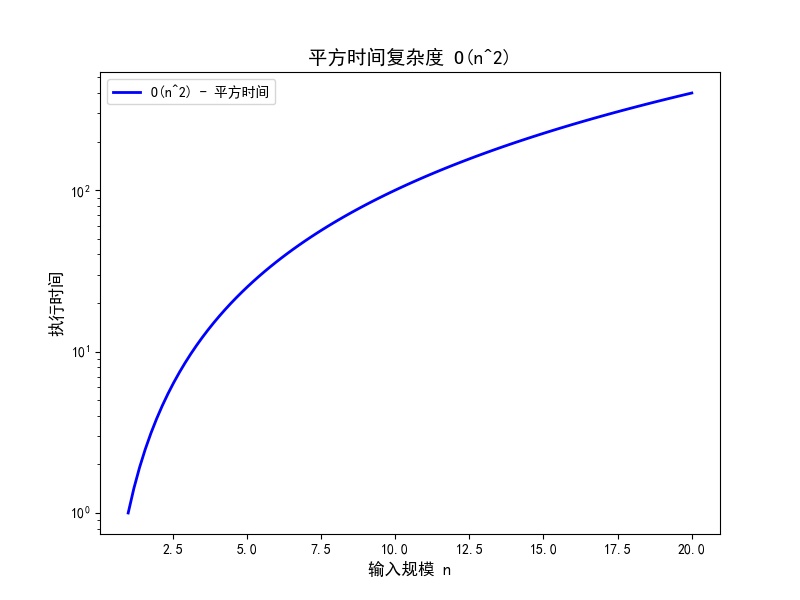
**O(n^2)**：平方时间，常见于简单的排序算法，如插入排序、冒泡排序等。
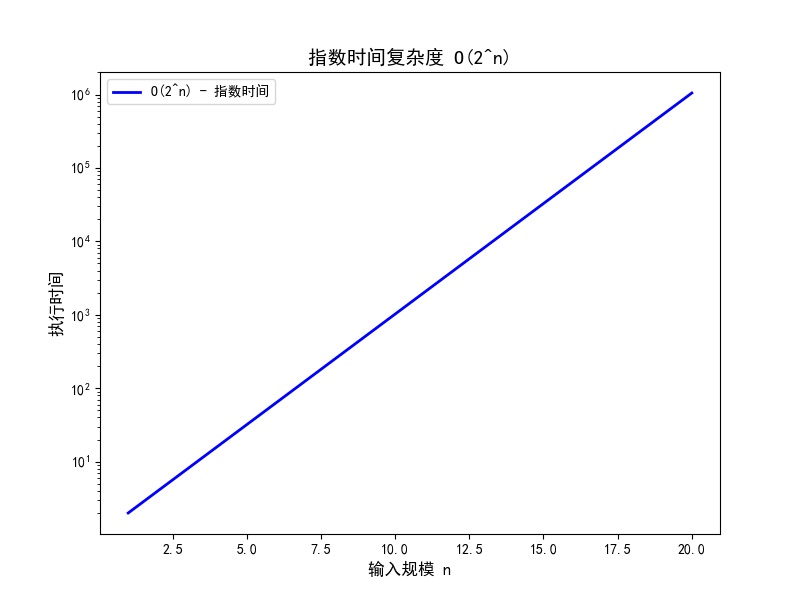
**O(2^n)**：指数时间，增长非常快，常见于暴力搜索算法。
**O(n!)**：阶乘时间，通常出现在全排列问题中。

时间复杂度示例：

**O(1)**：访问数组的某个元素。
**O(n)**：遍历数组，进行一次线性扫描。
**O(n^2)**：嵌套的两层循环，如冒泡排序。
**O(n log n)**：分治法排序算法，如快速排序、归并排序。

时间复杂度示例代码（遍历数组与双重循环）：

#include <iostream>
#include <vector>
using namespace std

;

// O(n) 示例：遍历数组
void linearExample(const vector<int>& arr) {
    for (int i = 0; i < arr.size(); i++) {
        cout << arr[i] << " ";
    }
}

// O(n^2) 示例：双重循环
void quadraticExample(const vector<int>& arr) {
    for (int i = 0; i < arr.size(); i++) {
        for (int j = 0; j < arr.size(); j++) {
            cout << arr[i] << "," << arr[j] << endl;
        }
    }
}

int main() {
    vector<int> arr = {1, 2, 3, 4};
    linearExample(arr);   // O(n)
    cout << endl;
    quadraticExample(arr); // O(n^2)
    return 0;
}