c++中的组合的概念

发表于 2024-10-18 分类于算法阅读次数：本文字数： 3k 阅读时长 ≈ 3 分钟

1. 什么是组合？

在数学中，组合是从一组元素中选择出若干个元素，不考虑元素的排列顺序。例如，假设有三个字母 ( {A, B, C} )，如果我们想要从中选择两个字母，组合的结果有：

AB, AC, BC

注意：组合与排列不同，组合只关心选择哪些元素，不考虑这些元素的顺序。因此，组合中的 AB 和 BA 被认为是相同的。

2. 组合的数学定义

组合的数学公式表示为：

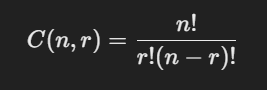
其中，C(n,r)表示从 n 个元素中选择 r 个元素的组合数。

n 表示总共有多少个元素。
r 表示从中选择几个元素。
n! 表示 n 的阶乘，即 n!=n×(n−1)×⋯×1。

示例：

从 5 个元素中选择 2 个进行组合，公式为：

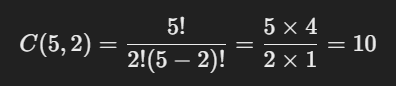
即 5 个元素中选择 2 个，共有 10 种不同的组合方式。

3. C++ 实现组合的基本思路

在 C++ 中，生成组合的基本思路是使用递归。我们可以使用以下两种方式来生成组合：

递归选择：对每个元素，考虑选取它还是不选取它，然后递归地生成剩余元素的组合。
循环遍历：通过固定第一个元素，然后递归处理剩余元素。

示例：生成一个数组的所有组合

示例代码：生成所有组合

#include <iostream>
using namespace std;

// 打印当前组合
void printCombination(int arr[], int comb[], int n, int r) {
    for (int i = 0; i < r; i++) {
        cout << comb[i] << " ";  // 输出当前组合中的元素
    }
    cout << endl;
}

// 递归生成组合的函数
void generateCombinations(int arr[], int comb[], int start, int index, int n, int r) {
    // 当组合中已经有了 r 个元素，打印该组合
    if (index == r) {
        printCombination(arr, comb, n, r);
        return;
    }

    // 从当前的 start 位置开始，选择剩余的元素进行组合
    for (int i = start; i <= n - (r - index); i++) {
        comb[index] = arr[i];  // 选择当前元素
        generateCombinations(arr, comb, i + 1, index + 1, n, r);  // 递归选择下一个元素
    }
}

int main() {
    int arr[] = {1, 2, 3, 4, 5};  // 要组合的数组
    int n = sizeof(arr) / sizeof(arr[0]);  // 数组元素个数
    int r = 3;  // 每次选择 3 个元素进行组合

    int comb[r];  // 存储当前组合的数组

    cout << "所有组合为：" << endl;
    generateCombinations(arr, comb, 0, 0, n, r);  // 调用生成组合的函数

    return 0;
}

详细注释与代码讲解：

printCombination 函数：当生成了一个完整的组合后，用该函数打印组合结果。组合存储在 comb[] 数组中。
generateCombinations 函数：这是递归生成组合的核心函数，它有以下参数：
- arr[]：存储要进行组合的元素。
- comb[]：存储当前选择的组合元素。
- start：表示当前在 arr[] 数组中选择元素的位置。
- index：当前在 comb[] 中已经填充的元素位置。
- n：数组 arr[] 中的元素个数。
- r：需要选择的元素个数。
  在每次递归中，它从 start 位置开始选择元素，并在递归过程中将选择的元素填入 comb[] 数组中。当 comb[] 中填满了 ( r ) 个元素时，打印该组合。

输出结果：

4. 组合的常见算法与应用

4.1 二项式系数

组合数 C(n, r) 也称为二项式系数。可以使用递归或动态规划来计算组合数。计算公式为：

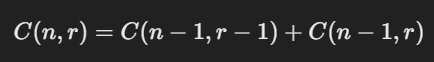
当 r = 0 或 r = n 时，组合数为 1。

4.2 递归计算组合数

下面是一个用递归实现计算 C(n, r) 的代码示例：

#include <iostream>
using namespace std;

// 递归计算组合数 C(n, r)
int combination(int n, int r) {
    if (r == 0 || r == n) {
        return 1;  // C(n, 0) = C(n, n) = 1
    }
    return combination(n - 1, r - 1) + combination(n - 1, r);
}

int main() {
    int n, r;
    cout << "输入 n 和 r：";
    cin >> n >> r;

    cout << "C(" << n << ", " << r << ") = " << combination(n, r) << endl;

    return 0;
}

输出结果：

输入 n 和 r：5 3
C(5, 3) = 10

4.3 组合的其他应用场景

组合问题在现实生活中有广泛的应用场景，例如：

彩票号码选择：从若干个号码中选择一定数量的号码进行组合。
团队选拔：从多人中选择特定数量的成员组成一个团队。

5. CSP-J 历年关于组合的题目

中国计算机学会（CSP-J）比赛中，组合问题也经常出现。以下是一些典型的题目：

题目1：组合生成

题目描述：

给定一个长度为 ( n ) 的数组，数组中包含 ( 1 ) 到 ( n ) 的整数，要求输出所有长度为 ( r ) 的组合。

解题思路：

使用递归方法生成所有长度为 ( r ) 的组合，类似于上面的示例代码。

题目2：组合数计算

题目描述：

输入两个整数 ( n ) 和 ( r )，计算组合数 ( C(n, r) )。

解题思路：

可以使用递归方法或者动态规划方法来计算组合数。

题目3：组合的计数

题目描述：

给定一个数组，数组中的元素可能有重复，要求计算可以从中选出若干个不同元素的组合数。

解题思路：

需要先对数组进行去重，然后计算不重复元素的组合。

题目4：特殊条件组合

题目描述：

给定一组元素，从中选出若干个元素组成组合，要求组合中的元素之和满足某种特定条件（如和为某个给定值）。

解题思路：

可以在生成组合的同时，判断组合元素的和是否满足条件。

6. 其他拓展知识

阶乘的递归计算

阶乘 ( n! ) 是计算组合数中的基础运算。我们可以使用递归方式计算阶乘。

示例代码：递归计算阶乘

#include <iostream>
using namespace std;

// 递归计算 n 的阶乘
int factorial(int n) {
    if (n == 0 || n == 1)
        return 1;
    return n * factorial(n - 1);
}

int main() {
    int n;
    cout << "输入一个数：";
    cin >> n;
    cout << n << "! = " << factorial(n) << endl;
    return 0;
}

输出结果：

输入一个数：5
5! = 120

7. 小结

组合是数学中从一

组元素中选择若干个元素的方式，不考虑顺序。

在 C++ 中生成组合可以使用递归与回溯的算法，通过递归遍历所有可能的组合。
组合问题是编程竞赛中的常见问题，结合递归与数学公式可以解决很多实际问题。
通过结合一些经典的 CSP-J 题目，可以巩固和应用组合的知识。

后续的学习中，可以结合更多题目进行练习，进一步掌握组合的生成和组合数的计算方法。